Exos sympas MP(*)
Re: Exos sympas MP(*)
Trois premiers chiffres en partant de la droite ou en partant de la gauche?
Re: Exos sympas MP(*)
Par exemple les 3 premiers chiffres de l'entier 123456789 est 123.
Re: Exos sympas MP(*)
[quote=Contrexemple post_id=1046224 time=1685092418 user_id=
$ $
Travail en series :
Soit $(a_n)_n \in (\mathbb R_+^*)^{\mathbb N}$ avec $\sum\limits_{n\in\mathbb N} a_n=+\infty$. A-t-on $\sum \limits_{n\in\mathbb N} \dfrac{a_n}{\sum \limits_{k=0}^n a_k} =+\infty$ ?
[/quote]
oui
si a(0)/S(0)+a(1)/S(1)+a(2)/S(2)+… +a(n)/S(n)+… converge , pour p<q
a(p+1)/S(p+1) + …+ a(q)/S(q) plus grand que (S(q)-S(p))/S(q)=1 - S(p)/S(q) pour q —->+oo
a(p+1)/S(p+1) + a(p+2)/S(p+2)+… serait plus grand que 1 contradiction car le reste tend vers 0
$ $
Travail en series :
Soit $(a_n)_n \in (\mathbb R_+^*)^{\mathbb N}$ avec $\sum\limits_{n\in\mathbb N} a_n=+\infty$. A-t-on $\sum \limits_{n\in\mathbb N} \dfrac{a_n}{\sum \limits_{k=0}^n a_k} =+\infty$ ?
[/quote]
oui
si a(0)/S(0)+a(1)/S(1)+a(2)/S(2)+… +a(n)/S(n)+… converge , pour p<q
a(p+1)/S(p+1) + …+ a(q)/S(q) plus grand que (S(q)-S(p))/S(q)=1 - S(p)/S(q) pour q —->+oo
a(p+1)/S(p+1) + a(p+2)/S(p+2)+… serait plus grand que 1 contradiction car le reste tend vers 0
Re: Exos sympas MP(*)
Salut,
$ $
Bijectivité de polynômes :
Soient $p=2^{127}-1$, $P\in \mathbb Z/p\mathbb Z[x]$ avec $\deg(P)=7$. A-t-on $P : \mathbb F_p \rightarrow \mathbb F_p$ qui n'est pas une fonction bijective ?
la question à un million de dollars :
Soit $n \in \mathbb N^*,n>3$. Existe-t-il une forme linéaire non triviale $f : H \rightarrow \mathbb R$ avec $H$ un sev de $M_n(\mathbb R)$ stable par multiplication, $\dim(H)>1$ et $\forall A,B \in H, f(A \times B)=f(A) \times f(B)$ ?
Bonne recherche.
$ $
Bijectivité de polynômes :
Soient $p=2^{127}-1$, $P\in \mathbb Z/p\mathbb Z[x]$ avec $\deg(P)=7$. A-t-on $P : \mathbb F_p \rightarrow \mathbb F_p$ qui n'est pas une fonction bijective ?
la question à un million de dollars :
Soit $n \in \mathbb N^*,n>3$. Existe-t-il une forme linéaire non triviale $f : H \rightarrow \mathbb R$ avec $H$ un sev de $M_n(\mathbb R)$ stable par multiplication, $\dim(H)>1$ et $\forall A,B \in H, f(A \times B)=f(A) \times f(B)$ ?
Bonne recherche.
Re: Exos sympas MP(*)
Salut,
$ $
Un résultat étrange sur les polynômes irréductibles :
Soit $P \in \mathbb Z[x]$ irreductible, avec $\exists (u,v) \in \mathbb C^2, P(u)=P(v)=0$ et $(|u|,|v|) \in\mathbb Q^2$.
A-t-on $|u|=|v|$ ?
Super équations fonctionnelles :
Soit $P \in\mathbb R[x]$ avec $P(x)= \sum \limits_{k=0}^n a_k x^k$ sans racines réelles.
Déterminer toutes les fonctions $f\in C^\infty (\mathbb R)$ avec : $\forall x \in \mathbb R, \sum\limits_{k=0}^n a_kf^k(x)=0$.
PS : $\forall x \in\mathbb R, f^0(x)=x,f^2(x)=f\circ f (x)$
Fonctions conservantes :
$f$ une fonction réelle, est conservante si, $\forall (a_n) \in \mathbb R^\mathbb N$ avec $\exists M>0, \forall n \in\mathbb N, |\sum \limits_{k=0}^n a_k| <M$ alors $\exists N>0, \forall n \in\mathbb N, |\sum \limits_{k=0}^n f(a_k)|<N$.
Trouver toutes les fonctions réelles conservantes.
Une étrange équation fonctionnelle sur les polynômes :
Determiner tous les polynômes $P \in \mathbb Z[x]$ avec $\forall a,b \in \mathbb N$ si $\gcd(a,b)=1$ alors $\gcd(P(a),P(b))=1$.
Je connais ton numéro de téléphone :
Montre que ton numéro de téléphone se trouve dans la séquence des décimales de $B=\dfrac 1 {2^{107}-1}$
PS : par exemple si $A=0.0714800331234567893781...$ et mon numéro est 0033 1 23 45 67 89 alors mon numéro est les décimales de $A$.
Bonne recherche.
$ $
Un résultat étrange sur les polynômes irréductibles :
Soit $P \in \mathbb Z[x]$ irreductible, avec $\exists (u,v) \in \mathbb C^2, P(u)=P(v)=0$ et $(|u|,|v|) \in\mathbb Q^2$.
A-t-on $|u|=|v|$ ?
Super équations fonctionnelles :
Soit $P \in\mathbb R[x]$ avec $P(x)= \sum \limits_{k=0}^n a_k x^k$ sans racines réelles.
Déterminer toutes les fonctions $f\in C^\infty (\mathbb R)$ avec : $\forall x \in \mathbb R, \sum\limits_{k=0}^n a_kf^k(x)=0$.
PS : $\forall x \in\mathbb R, f^0(x)=x,f^2(x)=f\circ f (x)$
Fonctions conservantes :
$f$ une fonction réelle, est conservante si, $\forall (a_n) \in \mathbb R^\mathbb N$ avec $\exists M>0, \forall n \in\mathbb N, |\sum \limits_{k=0}^n a_k| <M$ alors $\exists N>0, \forall n \in\mathbb N, |\sum \limits_{k=0}^n f(a_k)|<N$.
Trouver toutes les fonctions réelles conservantes.
Une étrange équation fonctionnelle sur les polynômes :
Determiner tous les polynômes $P \in \mathbb Z[x]$ avec $\forall a,b \in \mathbb N$ si $\gcd(a,b)=1$ alors $\gcd(P(a),P(b))=1$.
Je connais ton numéro de téléphone :
Montre que ton numéro de téléphone se trouve dans la séquence des décimales de $B=\dfrac 1 {2^{107}-1}$
PS : par exemple si $A=0.0714800331234567893781...$ et mon numéro est 0033 1 23 45 67 89 alors mon numéro est les décimales de $A$.
Bonne recherche.
Re: Exos sympas MP(*)
Bonjour,
$ $
D784 : Jeu de mots
(1) $ba\rightarrow a^2b$
(2) $a^2b\rightarrow ba$
(3) $ab\rightarrow b^2a^2$
A-t-on, en utilisant les régles (1), (2) et (3) : $\exists k \in\mathbb N, ba \rightarrow a b^k$ ?
D805 : De tels polynômes existent-ils ?
Y-a-t-il $P,Q \in \mathbb R_+[x]$ avec $\forall x \in \mathbb R, \sum\limits_{i=0}^{20} x^i=(x-2)^2P(x)+(x-3)^2 Q(x)$ ?
D806 : De tels polynômes existent-ils, encore ?
Y-a-t-il $P,Q \in \mathbb R_+[x]$ avec $\forall x \in \mathbb R, (\sum\limits_{i=0}^{20} x^i)^2=(x-2)^2P(x)+(x-3)^2 Q(x)$ ?
Bonne recherche.
$ $
D784 : Jeu de mots
(1) $ba\rightarrow a^2b$
(2) $a^2b\rightarrow ba$
(3) $ab\rightarrow b^2a^2$
A-t-on, en utilisant les régles (1), (2) et (3) : $\exists k \in\mathbb N, ba \rightarrow a b^k$ ?
D805 : De tels polynômes existent-ils ?
Y-a-t-il $P,Q \in \mathbb R_+[x]$ avec $\forall x \in \mathbb R, \sum\limits_{i=0}^{20} x^i=(x-2)^2P(x)+(x-3)^2 Q(x)$ ?
D806 : De tels polynômes existent-ils, encore ?
Y-a-t-il $P,Q \in \mathbb R_+[x]$ avec $\forall x \in \mathbb R, (\sum\limits_{i=0}^{20} x^i)^2=(x-2)^2P(x)+(x-3)^2 Q(x)$ ?
Bonne recherche.
Re: Exos sympas MP(*)
Bonjour,
D851-852 : Séries convergentes ?
851) A-t-on convergence de $\sum\limits_{n\in\mathbb N^*} \dfrac{\cos(\sqrt n+n)}{n}$?
852) A-t-on convergence de $\sum\limits_{n\in\mathbb N^*} \dfrac{\cos(\cos(\sqrt n)+n)}{n}$?
D875 : Un résultat général sur les fonctions croissantes
Soient $u,v,w,g,f \in C(\mathbb R_+,\mathbb R_+^*)$ fonctions croissantes, avec $f,g,u \in C^1(\mathbb R_+)$ et
$$\forall x \in \mathbb R_+ u(x)=f(x)\times v(x) +g(x) \times w(x)$$.
Montrer que : $$\forall x \in \mathbb R_+, \dfrac{u'(x)}{u(x)} \geq \min\left(\dfrac {g'(x)} {g(x)}, \dfrac{f'(x)}{f(x)}\right) $$.
Bonne recherche.
D851-852 : Séries convergentes ?
851) A-t-on convergence de $\sum\limits_{n\in\mathbb N^*} \dfrac{\cos(\sqrt n+n)}{n}$?
852) A-t-on convergence de $\sum\limits_{n\in\mathbb N^*} \dfrac{\cos(\cos(\sqrt n)+n)}{n}$?
D875 : Un résultat général sur les fonctions croissantes
Soient $u,v,w,g,f \in C(\mathbb R_+,\mathbb R_+^*)$ fonctions croissantes, avec $f,g,u \in C^1(\mathbb R_+)$ et
$$\forall x \in \mathbb R_+ u(x)=f(x)\times v(x) +g(x) \times w(x)$$.
Montrer que : $$\forall x \in \mathbb R_+, \dfrac{u'(x)}{u(x)} \geq \min\left(\dfrac {g'(x)} {g(x)}, \dfrac{f'(x)}{f(x)}\right) $$.
Bonne recherche.
Re: Exos sympas MP(*)
Bonjour,
$ $
D906 : Une équation fonctionnelle givrée.
Trouver toutes les fonctions $f \in C(\mathbb R)$ avec $\forall x \in \mathbb R, \sin(f(x))+2f(\sin(x))=3\sin(x)$.
D907 : Raffinement de Feit-Thomson ?
Soit $G=<a,b>$ un groupe fini, $o(G)=o(a)\times o(b)$ avec $<a> \cap <b>=\{e\}$ et $o(a)>1,o(b)>1$.
A-t-on $G$ non simple ?
D908 : Nouvelle propriété additive sur les espaces de Baire ?
Soient $(U_n)$ et $(V_n)$ des suites d'ouvert dense sous ensemble de $\mathbb R$.
A-t-on $\mathbb R=\bigcap \limits_{n \in \mathbb N} U_n+ \bigcap \limits_{n \in \mathbb N} V_n$ ?
Bonne recherche.
$ $
D906 : Une équation fonctionnelle givrée.
Trouver toutes les fonctions $f \in C(\mathbb R)$ avec $\forall x \in \mathbb R, \sin(f(x))+2f(\sin(x))=3\sin(x)$.
D907 : Raffinement de Feit-Thomson ?
Soit $G=<a,b>$ un groupe fini, $o(G)=o(a)\times o(b)$ avec $<a> \cap <b>=\{e\}$ et $o(a)>1,o(b)>1$.
A-t-on $G$ non simple ?
D908 : Nouvelle propriété additive sur les espaces de Baire ?
Soient $(U_n)$ et $(V_n)$ des suites d'ouvert dense sous ensemble de $\mathbb R$.
A-t-on $\mathbb R=\bigcap \limits_{n \in \mathbb N} U_n+ \bigcap \limits_{n \in \mathbb N} V_n$ ?
Bonne recherche.
Re: Exos sympas MP(*)
Salut,
En attendant la nouvelle année :
Pouvez finir de remplir, cette grille 10*10 préremplie, avec des dominos 2*1 ?
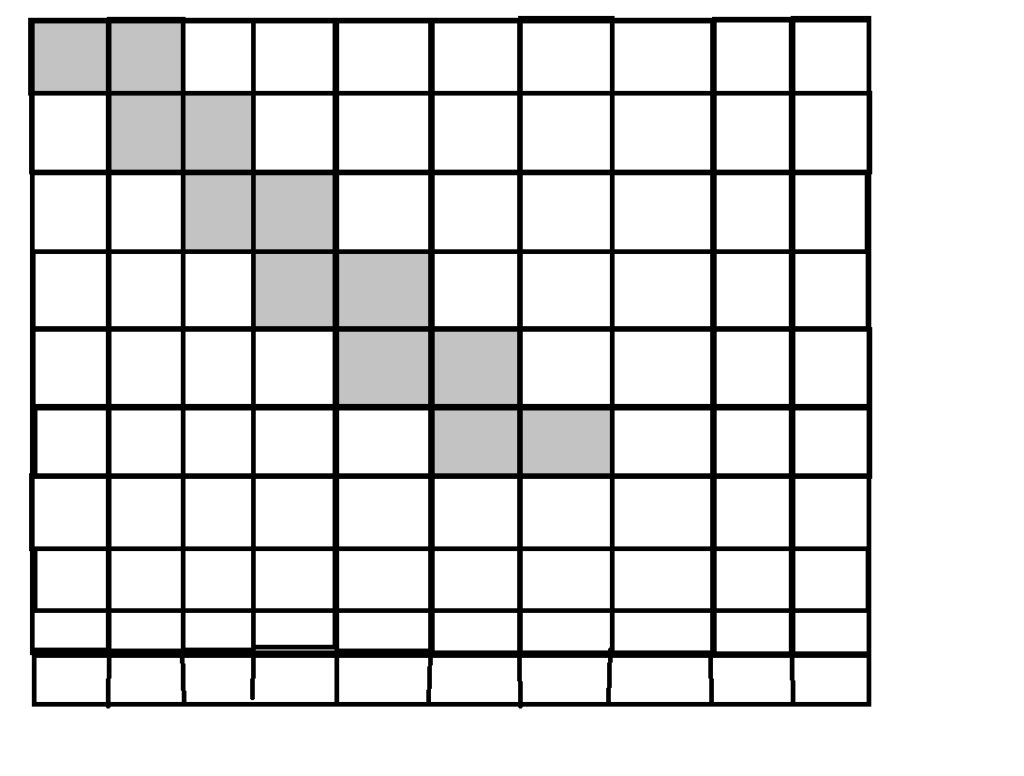
En attendant la nouvelle année :
Pouvez finir de remplir, cette grille 10*10 préremplie, avec des dominos 2*1 ?

