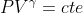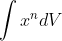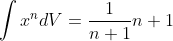Page 1 sur 1
Calcul du travail
Publié : 01 sept. 2021 22:49
par Azz77
Bonjour / Bonsoir à toutes et à tous !
Lors d'une de mes lectures hors cadre scolaire d'un livre sur la technologie des moteurs, je suis tombé sur une formule de calcul du travail d'une compression pour un moteur 4 temps que je n'arrive pas à comprendre. La voici :

Je ne comprend pas la démarche sachant qu'on part de W= -PdV
Merci d'avance
Re: Calcul du travail
Publié : 02 sept. 2021 15:47
par U46406
il vaudrait mieux que ce soit posté ou déplacé par un modérateur dans la section Physique :
viewforum.php?f=8
explique donc déjà quels calculs tu as vérifiés.
(As-tu moyen de rattacher ces notions à des supports de cours * que tu aurais à ta disposition ?)
Si tu es en DUT et que tu postes sur forum Prépas, c'est que tu veux aller après en prépaATS ??
*
Re: Calcul du travail
Publié : 02 sept. 2021 18:11
par Hibiscus
Que connais-tu des lois de Laplace ?
Re: Calcul du travail
Publié : 02 sept. 2021 18:52
par Azz77
En effet j'aimerais intégrer une prépa à la fin de l'année !
Et bien je sais qu'il s'agit d'une transformation adiabatique puisque
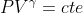
Donc après avoir divisé et multiplié par
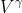
on peux sortir
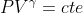
de l'intégral et on se retrouve avec une intégrale du type
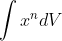
or
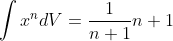
c'est dans mon développement que je n'arrive pas obtenir le même résultat.
Re: Calcul du travail
Publié : 02 sept. 2021 20:06
par Hibiscus
Il y a probablement une coquille dans tes étapes de calcul.
Auquel cas, pourquoi ne pas choisir de raisonner sans invoquer d'intégrales "calculatoires" (ou presque) et éviter ce type d'erreur ?
- Tu sais que $ PV^\gamma $ est constante
- Tu sais que la variation d'énergie élémentaire $ dU = qm C_v dT $ est égale au travail, puisque c'est une transformation adiabatique (avec $ qm=n $, en respectant les notations de l'énoncé)
- Tu vois donc sans même écrire d'intégrale compliquée (puisqu'elle porte sur $ dT $) que le travail reçu s'écrit:
$ W=qm C_v (T_2-T_1) $
Ce qui, avec la loi des gaz parfaits donne tout de suite $ W=\frac{(P_2V_2-P_1V_1)}{\gamma-1} $.
De là, tu peux insérer les notations de l'énoncé, notamment le $ \epsilon $ pour retrouver les deux expressions proposées.