Re: Exos sympas MPSI
Publié : 10 juin 2024 00:08
Bonsoir,
$ $
D850 : Limite de suites récurrentes non linéaires.
Soit $f \in C(\mathbb R,\mathbb R)$ bijective, $u_0=u_1=1$ et $\forall n \in \mathbb N, u_{n+2}=\dfrac 1 2 f^{-1}\left(\dfrac {f(u_{n+1})} 2 +\dfrac{f(u_{n})}2\right) +1$.
A-t-on $(u_n)$ converge ?
D853 : Traduction de o à O.
Peut-on construire une condition $A$ qui ne s'exprime qu'avec des $O$ et telles que :
Pour toutes $(u_n),(v_n)$ suites réels strictement positives on a : $o(u_n)=o(v_n) \text{ iff } A(u_n,v_n)$.
D860 : Dominos en fleurs et non connexes CNS
Soit G une grille de taille m*n.
On dispose de 2 sortes de dominos en fleurs et non connexes comme ici
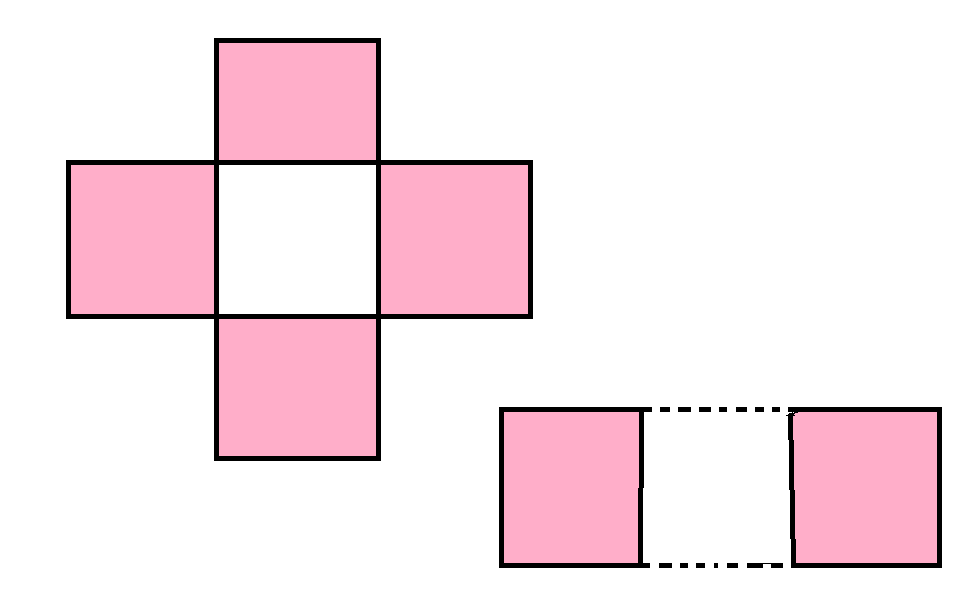
Déterminer une CNS sur m et n, pour que G puisse être recouvert avec ces 2 sortes de dominos.
D874 : Dominos diagonaux CNS
On dispose de dominos diagonaux comme celui là :
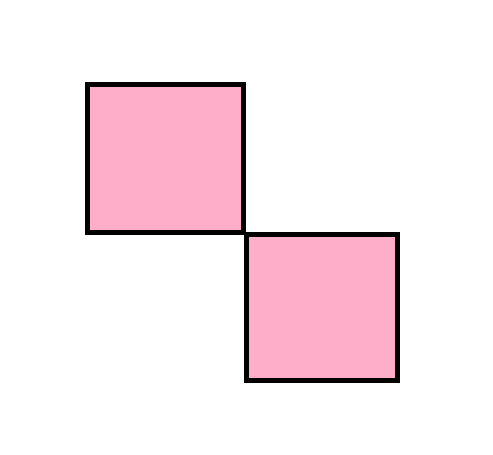
Déterminer une CNS sur n et m, pour pouvoir couvrir avec une grille rectangle de taille n*m.
Bonne recherche.
$ $
D850 : Limite de suites récurrentes non linéaires.
Soit $f \in C(\mathbb R,\mathbb R)$ bijective, $u_0=u_1=1$ et $\forall n \in \mathbb N, u_{n+2}=\dfrac 1 2 f^{-1}\left(\dfrac {f(u_{n+1})} 2 +\dfrac{f(u_{n})}2\right) +1$.
A-t-on $(u_n)$ converge ?
D853 : Traduction de o à O.
Peut-on construire une condition $A$ qui ne s'exprime qu'avec des $O$ et telles que :
Pour toutes $(u_n),(v_n)$ suites réels strictement positives on a : $o(u_n)=o(v_n) \text{ iff } A(u_n,v_n)$.
D860 : Dominos en fleurs et non connexes CNS
Soit G une grille de taille m*n.
On dispose de 2 sortes de dominos en fleurs et non connexes comme ici

Déterminer une CNS sur m et n, pour que G puisse être recouvert avec ces 2 sortes de dominos.
D874 : Dominos diagonaux CNS
On dispose de dominos diagonaux comme celui là :

Déterminer une CNS sur n et m, pour pouvoir couvrir avec une grille rectangle de taille n*m.
Bonne recherche.