Les dattes à Dattier

[GaBuZoMeu]

Grognon, oty20 ? Comme je l'ai dit, je n'ai pas de démonstration, pas trop envie d'en chercher d'ailleurs, mais j'ai des images.

Le graphe de $ f $ d'abord



et puis les 100000 premiers termes de la suite des $ f^n(0.5) $

[GaBuZoMeu]

Caramba, encore raté ! Que vaut ta fonction pour
$ x= \tan\left(\frac{\pi}{2}\sin\left(\frac{\pi}{2}-1\right)\right) $ ?

[btsix]

229

SPOILER:

$ \overline{A} $ est compact bien sûr, mais pas nécessairement gros :

$ A := \{ 3^{-n} + 3^{-m} \: | \: (n, m) \in \mathbb{N}^2 \} $
$ \overline{A} = A \sqcup \{3^{-p} \: | \: p \in \mathbb{N} \} \sqcup \{ 0 \} $

[GaBuZoMeu]

Caramba, encore raté ! Cette fois, tu t'en es aperçu toi même. Je vois que tu es vexé (ton "GaGa").

Je te laisse revoir la fonction que j'ai écrite pour vérifier qu'elle va bien de $ ]0,1[ $ dans $ ]0,1[ $ (ouvert !).

[btsix]

230

SPOILER:

Oui :

$ 0 = (230 - 230) \times (230 + 230 + 230 + 230 + 230) $.

Soit $ n \in \mathbb{N}^{*} $.
L'ensemble $ \{ \frac{2^p}{3^q} \: | \: (p, q) \in \mathbb{N}^2 \} $ est dense dans $ \mathbb{R}_{+} $.
On dispose ainsi de $ (p, q) \in \mathbb{N}^2 $ tel que $ \log_{2} (n) < \frac{2^p}{3^q} < \log_{2} (n+1) $, donc tel que $ n = \lfloor 2^{\frac{2^p}{3^q}} \rfloor = \lfloor g^q(f^p(\frac{230+230}{230})) \rfloor + (230 - 230) + (230 - 230) $ où $ f $ et $ g $ sont les fonctions carré et racine cubique.

[btsix]

231

SPOILER:

Non :
Par récurrence : $ \forall n \in \mathbb{N} $,$ f^n(1) \equiv \left \{ \begin{split} 1 \; [\text{mod} \; 4] \; & \mbox{ si } n \; \text{est pair} \\ 2 \; [\text{mod} \; 4] \; & \mbox{ si } n \; \text{est impair}\end{split} \right. $.
Donc $ \forall n \in \mathbb{N} $, $ 2^{115} \nmid f^n(1) $, puis $ \forall n \in \mathbb{N} $, $ 2^{230} \nmid [f^n(1)]^2 $, puis $ \forall n \in \mathbb{N}^{*} $, $ 2^{231} \nmid [f^{n-1}(1)]^2 $, puis $ \forall n \in \mathbb{N}^{*} $,$ f^n(1) \not\equiv 1 \; [\text{mod} \; 2^{231}] $.

[Siméon]

2/ Et le cas N pair (tu as utilisé une 1/2 lignes, il te reste une demi lignes) ?

La 190 montrait déjà que la condition $ N $ impair est nécessaire.

SPOILER:

En fait $ \sum_{a \in \mathbb Z/2n\mathbb Z} a = n $.

Pour résumer la 228, il me semble que tu as perdu un Choco BN. Non ?

[btsix]

225

SPOILER:

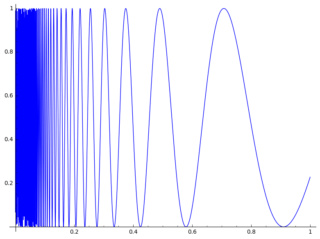
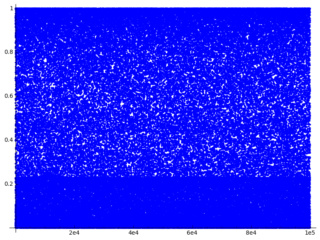
Non :

Supposons que $ R $ peut être décrite à l'aide des opérations $ + $, $ - $, $ \times $, $ / $, $ E $. Il existe une fonction $ f $, composée de ces opérations, qui prolonge $ R $ sur $ \mathbb{R} $ sauf en un nombre fini de points. $ f $ est continue sur l'intérieur de son domaine de définition $ \mathring{D_f} $, qui est une réunion d'intervalles non vides et non réduits à un point. En particulier, par densité de $ \mathbb{Q}(\sqrt{2}) $, f est continue en un point $ x_0 = a_0 + b_0\sqrt{2} $ de $ \mathbb{Q}(\sqrt{2}) $.

Pourtant :

Soit $ \eta > 0 $ tel que $ f $ est bien définie sur $ ]x_0 - \eta, x_0 + \eta[ $.
On dispose de $ (r,s) \in \mathbb{Q}^2 $ vérifiant $ |r - s \sqrt{2}| \le 1 $ et $ |r + s \sqrt{2}| > \frac{1}{\eta} $.
Soit $ (c,d) \in \mathbb{Q}^2 $ tel que $ \frac{1}{r + s \sqrt{2}} = c + d \sqrt{2} $.
Posons $ x = x_0 + c + d \sqrt{2} $.
On a $ |x - x_0| < \eta $ et $ |f(x) - f(x_0)| = |R(x) - R(x_0)| = |c - d \sqrt{2}| = \frac{1}{| r - s \sqrt{2} |} \ge 1 $.
Absurde.

[Siméon]

Merci, mais ni les dattes ni les Choco BN ne sont bons pour mon régime. Voici tout de même une solution pour le 228 sans détailler :

SPOILER:

Soit $a$ un réel dont le développement dyadique contient toute suite finie de $0$ et de $1$. Alors $\left\{\cos(2^n a\pi) ; n \in \mathbb N \right\}$ est dense dans $]-1,1[$. Ceci correspond à la suite engendrée par $g: c \mapsto 2 c^2 - 1$ en partant de $\cos(a\pi)$. Il suffit donc de considérer $f = \varphi \circ g\circ \varphi^{-1}$ où $\varphi$ est un homéomorphisme quelconque de $]-1;1[$ dans $\mathbb R$ tel que $\varphi(\cos(a\pi)) = 0$.

$ $

[Siméon]

Contrairement à Gabuzomeu j'ai donné une démonstration (à trous certes, mais faciles à combler). Pour le reste, je ne comprends rien à ton délire...