Transfo parfait à vide
Re: Transfo parfait à vide
Ça y est, je pense avoir trouvé la réponse (dans mes anciens cours). Le flux est dû au champ magnétique dû aux courant fictifs (ou liés à la matière):
Les courants fictifs sont les courants créés par les moments magnétiques des molécules du matériau ferromagnétique.
Appelons $ \vec{B'} $ le champ magnétique créé par les courants fictifs. On a
$ \vec{B'}=\overrightarrow{rot}\vec{A'} $
avec
$ \vec{A'}=\frac{\mu_0}{4\pi}\iiint\frac{\overrightarrow{rot}\vec{M}}{r} dV + \frac{\mu_0}{4\pi}\iint \frac{\vec{M}\wedge \vec{N}}{r}\overrightarrow{dS} $
Cela permet de calculer $ \vec{B'} $ qui est le champ magnétique dans le circuit magnétique.
Ce $ \vec{B'} $ est dû à l'aimantation $ \vec{M} $ non nulle, même si $ \vec{M} $ est induite et que l'excitation $ \vec{H} $ est nulle, car quand le milieu est parfait on a $ \vec{M} = \kappa \vec{H} $ avec $ \mu_r = 1 + \kappa $.
Donc on imagine aisément $ \vec{M} $ différent de $ \vec{0} $ même pour $ \vec{H} $ égal à $ \vec{0} $, puisque $ \kappa\rightarrow \infty $
Donc $ \vec{M} $ différent de $ \vec{0} $, donc $ \vec{B'} $ différent de $ \vec{0} $, donc un flux différent de 0.
Du coup, pas d'intervention du champ magnétique créé par le champ électrique variable créé par la tension variable... je ne vois donc pas l'utilité de l'expression littérale "flux forcé par la tension"....
Les courants fictifs sont les courants créés par les moments magnétiques des molécules du matériau ferromagnétique.
Appelons $ \vec{B'} $ le champ magnétique créé par les courants fictifs. On a
$ \vec{B'}=\overrightarrow{rot}\vec{A'} $
avec
$ \vec{A'}=\frac{\mu_0}{4\pi}\iiint\frac{\overrightarrow{rot}\vec{M}}{r} dV + \frac{\mu_0}{4\pi}\iint \frac{\vec{M}\wedge \vec{N}}{r}\overrightarrow{dS} $
Cela permet de calculer $ \vec{B'} $ qui est le champ magnétique dans le circuit magnétique.
Ce $ \vec{B'} $ est dû à l'aimantation $ \vec{M} $ non nulle, même si $ \vec{M} $ est induite et que l'excitation $ \vec{H} $ est nulle, car quand le milieu est parfait on a $ \vec{M} = \kappa \vec{H} $ avec $ \mu_r = 1 + \kappa $.
Donc on imagine aisément $ \vec{M} $ différent de $ \vec{0} $ même pour $ \vec{H} $ égal à $ \vec{0} $, puisque $ \kappa\rightarrow \infty $
Donc $ \vec{M} $ différent de $ \vec{0} $, donc $ \vec{B'} $ différent de $ \vec{0} $, donc un flux différent de 0.
Du coup, pas d'intervention du champ magnétique créé par le champ électrique variable créé par la tension variable... je ne vois donc pas l'utilité de l'expression littérale "flux forcé par la tension"....
Papouille2, Responsable département projets dans le privé
Re: Transfo parfait à vide
en fait la question est nulle est non avenue puisque le modèle parfait n'existe pas 
mais a priori d'un point de vue "mathématique" le produit $ \mu_r H $ avec $ \mu_r $ qui est "très grand" et $ H $ très petit est une forme indéterminée
donc $ B $ peut tout à fait être non nul ...
Dans la pratique effectivement, comme on impose la tension on est à flux forcé dans ce cas là la source fournit le courant qui va bien pour créer $ H $ (et donc $ B $ puisque les deux sont liés)
voici quelques propositions "d'explication"
Une manière d'aborder la question : le transformateur peut aussi se modéliser comme deux circuits magnétiques parfaitement couplés c'est à dire avec $ M^2=L_1L_2 $.
Dans ce cas, il est équivalent à vide à l'inductance $ L_1 $ et cette inductance tend vers l'infini dans le modèle parfait si bien que $ I_1=\frac{U_1}{L_1\omega} $ tend vers 0 ...
Autre manière de voir les choses :
si on travaille avec la réluctance, on a
$$ \mathcal{R}\phi_C=n_1i_1-n_2i_2 $$
comme pour un circuit magnétique "simple", on a $ \mathcal{R}=\frac{l}{\mu_r\mu_0 S} $, l'approximation $ \mu_R\rightarrow \infty $ entraîne que $ n_1i_1-n_2i_2=0 $. Dans la réalité, bien entendu ce n'est pas le cas et on a $ n_1i_1-n_2i_2=n_1 i_{1,0} $ où $ i_{1,0} $ est le courant d'excitation nécessaire à la création du champ et qui est donc aussi le courant "à vide" (qui tend vers 0 pour le transfo parfait)
NB : je n'ai fait que survoler la discussion mais cette histoire de courant d'aimantations permet juste d'expliquer le lien entre $ \vec{B} $ et $ \vec{H} $ je ne suis pas sûr qu'elle permette de répondre à la question.
mais a priori d'un point de vue "mathématique" le produit $ \mu_r H $ avec $ \mu_r $ qui est "très grand" et $ H $ très petit est une forme indéterminée
donc $ B $ peut tout à fait être non nul ...
Dans la pratique effectivement, comme on impose la tension on est à flux forcé dans ce cas là la source fournit le courant qui va bien pour créer $ H $ (et donc $ B $ puisque les deux sont liés)
voici quelques propositions "d'explication"
Une manière d'aborder la question : le transformateur peut aussi se modéliser comme deux circuits magnétiques parfaitement couplés c'est à dire avec $ M^2=L_1L_2 $.
Dans ce cas, il est équivalent à vide à l'inductance $ L_1 $ et cette inductance tend vers l'infini dans le modèle parfait si bien que $ I_1=\frac{U_1}{L_1\omega} $ tend vers 0 ...
Autre manière de voir les choses :
si on travaille avec la réluctance, on a
$$ \mathcal{R}\phi_C=n_1i_1-n_2i_2 $$
comme pour un circuit magnétique "simple", on a $ \mathcal{R}=\frac{l}{\mu_r\mu_0 S} $, l'approximation $ \mu_R\rightarrow \infty $ entraîne que $ n_1i_1-n_2i_2=0 $. Dans la réalité, bien entendu ce n'est pas le cas et on a $ n_1i_1-n_2i_2=n_1 i_{1,0} $ où $ i_{1,0} $ est le courant d'excitation nécessaire à la création du champ et qui est donc aussi le courant "à vide" (qui tend vers 0 pour le transfo parfait)
NB : je n'ai fait que survoler la discussion mais cette histoire de courant d'aimantations permet juste d'expliquer le lien entre $ \vec{B} $ et $ \vec{H} $ je ne suis pas sûr qu'elle permette de répondre à la question.
Sciences Physiques,MP*-ex PSI* Corneille Rouen
Re: Transfo parfait à vide
Bonjour à vous 2,
Puisque la discussion continue et que j'ai visiblement un peu de retard dans mes révisions par rapport à Papouille2 j'aimerais pointer qu'une forme indéterminée peut en cacher une autre.
j'aimerais pointer qu'une forme indéterminée peut en cacher une autre.
En effet si l'on prend la relation liant permittivité et perméabilité dans le vide :
$$ \varepsilon_{0}.\mu_{0}=\frac{1}{c^{2}} $$
et qu'on s'amuse à l'exprimer différemment avec $ \varepsilon_{0}=\frac{\varepsilon_{}}{\varepsilon_{r}} $ et $ \mu_{0}=\frac{\mu_{}}{\mu_{r}} $ cela nous conduit à cette équation:
$$ \varepsilon_{r}.\mu_{r}=\varepsilon_{}.\mu_{}.c^{2} $$
A droite une quantité à priori finie (caractéristiques du matériau, célérité de la lumière) et à gauche un produit dont un des termes est $ \infty $
Les approximations successives amènent souvent les auteurs à réintroduire petit à petit dans leur littérature des éléments qu'ils avaient négligés pour rendre les modèles plus "réalistes".
En tout cas merci à vous deux pour ces rappels en accéléré
Puisque la discussion continue et que j'ai visiblement un peu de retard dans mes révisions par rapport à Papouille2
En effet si l'on prend la relation liant permittivité et perméabilité dans le vide :
$$ \varepsilon_{0}.\mu_{0}=\frac{1}{c^{2}} $$
et qu'on s'amuse à l'exprimer différemment avec $ \varepsilon_{0}=\frac{\varepsilon_{}}{\varepsilon_{r}} $ et $ \mu_{0}=\frac{\mu_{}}{\mu_{r}} $ cela nous conduit à cette équation:
$$ \varepsilon_{r}.\mu_{r}=\varepsilon_{}.\mu_{}.c^{2} $$
A droite une quantité à priori finie (caractéristiques du matériau, célérité de la lumière) et à gauche un produit dont un des termes est $ \infty $
Les approximations successives amènent souvent les auteurs à réintroduire petit à petit dans leur littérature des éléments qu'ils avaient négligés pour rendre les modèles plus "réalistes".
En tout cas merci à vous deux pour ces rappels en accéléré
отец (un autre père ENSICAENnais) сынок (& fils PCSI▸PC▸PC* 2020-23 à B.Pascal (63) ➠ EC Lille) и Дух мира  (& esprit de 🕊)
(& esprit de 🕊)
Re: Transfo parfait à vide
Bonjour,
Jean, merci pour vos explications. Mais si j'ai bien compris elles ont pour objet de démontrer qu'au passage à la limite infinie de $ \mu_r $ on obtient $ i_1=0 $. Ce n'est pas l'objet de mon interrogation. Mon interrogation est : d'où pourrait venir le champ $ \vec{B} $ si le courant $ i_1=0 $.
Mon dernier post vise en fait à tirer les conséquences d'un passage à la limite infinie de $ \mu_r $. S'il n'y a pas de courant vrais ($ i_1=0 $), il reste les courants liés à la matière. Le champ $ \vec{B} $ viendrait exclusivement, dans le cas où $ \mu_r\rightarrow \infty $ du champ aimantation $ \vec{M} $.
Je dois continuer à réfléchir sur le sujet, car je ne vois pas où intervient la tension lors du passage à la limite de $ \mu_r $.
Soit dit en passant, et cela pourrait faire l'objet d'un nouveau post, le professeur en question m'a dit qu'un transfo parfait ne peut pas fonctionner, même théoriquement : un transfo parfait n'a pas de fuite (couplage parfait). Or le vecteur de Poynting passe en dehors du circuit magnétique, donc est nécessairement généré par les lignes du champ $ \vec{B} $ situées à l'exterieur du circuit magnétique. Ce champ étant nul à l'extérieur du circuit magnétique sans fuite, le vecteur de Poynting l'est aussi : en charge, un transformateur parfait ne peut théoriquement pas fonctionner puisqu'il n'a pas de fuite du champ $ \vec{B} $ (je crois que cela a fait l'objet d'une publication dans le BUP par des professeurs de Kleber à Strasbourg).
Jean, merci pour vos explications. Mais si j'ai bien compris elles ont pour objet de démontrer qu'au passage à la limite infinie de $ \mu_r $ on obtient $ i_1=0 $. Ce n'est pas l'objet de mon interrogation. Mon interrogation est : d'où pourrait venir le champ $ \vec{B} $ si le courant $ i_1=0 $.
Mon dernier post vise en fait à tirer les conséquences d'un passage à la limite infinie de $ \mu_r $. S'il n'y a pas de courant vrais ($ i_1=0 $), il reste les courants liés à la matière. Le champ $ \vec{B} $ viendrait exclusivement, dans le cas où $ \mu_r\rightarrow \infty $ du champ aimantation $ \vec{M} $.
Je dois continuer à réfléchir sur le sujet, car je ne vois pas où intervient la tension lors du passage à la limite de $ \mu_r $.
Soit dit en passant, et cela pourrait faire l'objet d'un nouveau post, le professeur en question m'a dit qu'un transfo parfait ne peut pas fonctionner, même théoriquement : un transfo parfait n'a pas de fuite (couplage parfait). Or le vecteur de Poynting passe en dehors du circuit magnétique, donc est nécessairement généré par les lignes du champ $ \vec{B} $ situées à l'exterieur du circuit magnétique. Ce champ étant nul à l'extérieur du circuit magnétique sans fuite, le vecteur de Poynting l'est aussi : en charge, un transformateur parfait ne peut théoriquement pas fonctionner puisqu'il n'a pas de fuite du champ $ \vec{B} $ (je crois que cela a fait l'objet d'une publication dans le BUP par des professeurs de Kleber à Strasbourg).
Papouille2, Responsable département projets dans le privé
Re: Transfo parfait à vide
J'ai exhumé une formule qui établit la relation entre les courants vrais, les courants fictifs, et $ \mu_r $:
$ \mu_r=\frac {\sum(courants - vrais) + \sum(courants - fictifs)} {\sum(courants-vrais)} $.
Puisque $ \mu_r $ est infini et $ \sum(courants-vrais) $ est nul, il reste des courants fictifs finis, qui seraient donc responsables de $ \vec{B} $.
Reste encore à établir le lien entre la tension et les courants fictifs
$ \mu_r=\frac {\sum(courants - vrais) + \sum(courants - fictifs)} {\sum(courants-vrais)} $.
Puisque $ \mu_r $ est infini et $ \sum(courants-vrais) $ est nul, il reste des courants fictifs finis, qui seraient donc responsables de $ \vec{B} $.
Reste encore à établir le lien entre la tension et les courants fictifs
Papouille2, Responsable département projets dans le privé
Re: Transfo parfait à vide
Le transfo parfait est une vue de l'esprit, l'équation aux courants:Papouille2 a écrit : ↑06 janv. 2023 12:38.../...Mon interrogation est : d'où pourrait venir le champ $ \vec{B} $ si le courant $ i_1=0 $.
$ n_{1}.i_{1}-n_{2}.i_{2}=0 \ \text{ (3)} $ est vraie $ \forall t $. C'est à dire qu'ils sont en opposition de phase, il en va de même pour le champ inducteur (resp. induit) du primaire en opposition instantanée avec le champ induit (resp. inducteur) du secondaire puisque la Réluctance est nulle. Il n'y a pas de déphasage, aucun "glissement". Bref tout se passe comme si le flux "net" est nul (superposition des effets des bobines du primaire et du secondaire) dans le matériau.
C'est à mon avis une autre façon de voir purement fictive mais bon ...
Puisque le "flux "net" est nul" (celui qui serait créée par le champ magnétique lui même induit par le courant) on l'attribue abusivement à la tension.Papouille2 a écrit : ↑06 janv. 2023 12:38.../... je ne vois pas où intervient la tension lors du passage à la limite de $ \mu_r $.
Tout est fictif en effetPapouille2 a écrit : ↑06 janv. 2023 13:49.../... Reste encore à établir le lien entre la tension et les courants fictifs
Dernière modification par H2Fooko le 07 janv. 2023 11:43, modifié 1 fois.
отец (un autre père ENSICAENnais) сынок (& fils PCSI▸PC▸PC* 2020-23 à B.Pascal (63) ➠ EC Lille) и Дух мира  (& esprit de 🕊)
(& esprit de 🕊)
Re: Transfo parfait à vide
en fait, on ne se comprend pas car mon propos est qu'avec $ \mu_r $ très grand, un tout petit courant (ou un très petit $ H $) suffit à créer le flux. En première approximation, on le considère nul mais il ne l'est pas vraiment.
Sciences Physiques,MP*-ex PSI* Corneille Rouen
Re: Transfo parfait à vide
Bonjour Jean, H2Fooko,
Oui. Le mieux est finalement de dire que i1 est infiniment proche de 0 sans être nul (infiniment petit) et crée B.
D'autant plus que dans la théorie du transformateur parfait, rien n'indique que le circuit doit être ferromagnétique : Je fais donc fausse route en allant chercher du côté de l'aimantation pour expliquer B.
Le flux net est nul, oui. Cela m'a interpellé dés le départ aussi, mais ai laissé ce paradoxe de côté en espérant pouvoir le résoudre une fois élucidé la question du flux "forcé par la tension". Donc effectivement peut-être qu'on l'attribue à la tension à défaut de pouvoir l'attribuer au courant (génant: car je préfère dire que le courant est un infiniment petit plutôt que dire qu'il est nul. À mon avis c'est cela qui doit résoudre le paradoxe: infiniment petit ne veut pas dire nul, et on dit abusivement que le courant est nul).
Oui. Le mieux est finalement de dire que i1 est infiniment proche de 0 sans être nul (infiniment petit) et crée B.
D'autant plus que dans la théorie du transformateur parfait, rien n'indique que le circuit doit être ferromagnétique : Je fais donc fausse route en allant chercher du côté de l'aimantation pour expliquer B.
Le flux net est nul, oui. Cela m'a interpellé dés le départ aussi, mais ai laissé ce paradoxe de côté en espérant pouvoir le résoudre une fois élucidé la question du flux "forcé par la tension". Donc effectivement peut-être qu'on l'attribue à la tension à défaut de pouvoir l'attribuer au courant (génant: car je préfère dire que le courant est un infiniment petit plutôt que dire qu'il est nul. À mon avis c'est cela qui doit résoudre le paradoxe: infiniment petit ne veut pas dire nul, et on dit abusivement que le courant est nul).
Papouille2, Responsable département projets dans le privé
Re: Transfo parfait à vide
Bonjour à vous 2 (et à ceux qui suivent de loin  )
)
Oui je suis d'accord d'ailleurs on voit sur certains sites anglophones des approches un peu différentes:
https://www.electricaleasy.com/2014/03/ ... stics.html
Notamment le paragraphe à côté de cette figure :
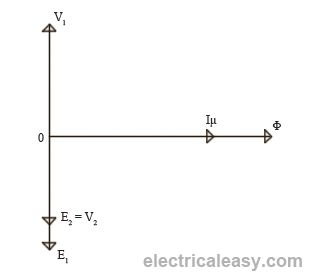
où le courant magnétisant est une conséquence de la tension appliquée au primaire.
Vu comme ça (l'angle de d'approche de l'auteur anglophone) c'est la tension qui est à la génèse de tout !
(d'où l'expression "Flux forcé par la tension")
PS : d'ailleurs à relire le post de Jean c'est bien cela :
$$ \Phi_{c}=\frac{1}{n_{1}}\int_{}^{}v_{1}\ dt $$
En simplifiant le système d'équations on a supprimé le lien entre $ v $ et $ i $ le courant qui va bien
Oui je suis d'accord d'ailleurs on voit sur certains sites anglophones des approches un peu différentes:
https://www.electricaleasy.com/2014/03/ ... stics.html
Notamment le paragraphe à côté de cette figure :

où le courant magnétisant est une conséquence de la tension appliquée au primaire.
Vu comme ça (l'angle de d'approche de l'auteur anglophone) c'est la tension qui est à la génèse de tout !
(d'où l'expression "Flux forcé par la tension")
PS : d'ailleurs à relire le post de Jean c'est bien cela :
ainsi que le contenu du premier lien puisque du système d'équation (1) on tire :Kieffer Jean a écrit : ↑04 janv. 2023 21:59.../... Dans la pratique effectivement, comme on impose la tension on est à flux forcé dans ce cas là la source fournit le courant qui va bien pour créer $ H $ (et donc $ B $ puisque les deux sont liés) .../...
$$ \Phi_{c}=\frac{1}{n_{1}}\int_{}^{}v_{1}\ dt $$
En simplifiant le système d'équations on a supprimé le lien entre $ v $ et $ i $ le courant qui va bien
Dernière modification par H2Fooko le 07 janv. 2023 19:17, modifié 3 fois.
отец (un autre père ENSICAENnais) сынок (& fils PCSI▸PC▸PC* 2020-23 à B.Pascal (63) ➠ EC Lille) и Дух мира  (& esprit de 🕊)
(& esprit de 🕊)
Re: Transfo parfait à vide
Au passage et concernant ma remarque du 6/1 à 12:38 sur les transformateurs parfaits et le vecteur de Poynting : si rien n'indique que le circuit magnétique d'un transfo parfait doit être ferromagnétique, alors on devrait penser à une idéalisation du transfo parfait comme étant une généralisation du cas où 2 spires sont superposées l'une à l'autre, l'une formant le circuit électrique primaire, l'autre le secondaire. Pas de ferromagnétisme ici, et toutes les équations restent vérifiées, sans que l'on ait besoin d'une reluctance nulle ou d'une perméabilité infinie dans le circuit magnétique ainsi formé. Le couplage est parfait, pas de fuite, et le vecteur de Poynting circule bien entre les deux spires.
Papouille2, Responsable département projets dans le privé
